A Kruskal-Wallis test uses sample data to determine if a numeric outcome variable with any distribution differs across two or more independent groups. This test is a non-parametric alternative to the one-way ANOVA and can be run when the data fails the normality assumption or if the sample sizes in each group are too small to assess normality.
Similar to the Mann-Whitney U test, which can be run on two groups, this test compares the sum of the ranks of the observations. The Kruskal-Wallis test does not test specifically if the mean or median of the groups differ, only if the overall distributions are significantly different or not.
Assumptions:
Hypotheses:
Ho: The population distributions do not differ across groups.
HA: The population distributions do differ across groups.
Example: How to run in RStudio
This example tests if cats have a different distribution of ages compared to dogs in an animal shelter.
Dataset used in video
R script file used in video
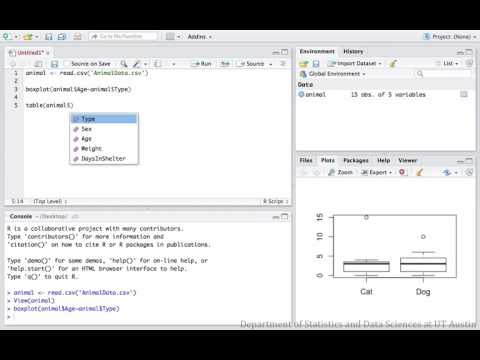

Sample conclusion: We found no evidence to suggest that the distributions of the ages of dogs and cats at the shelter differ (p=0.91).