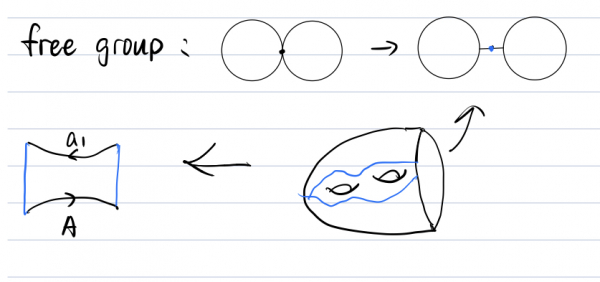
We can representing closed surfaces by identifying sides of a polygon:
Expressing an element gg in a group GG as a product of k commutators is the same as finding a connected orientable surface SS of genus kk with one boundary, and a map f:S→Xf:S→X for a space XX with π1(X)=Gπ1(X)=G so that f(∂S)f(∂S) represents the conjugacy class of gg.
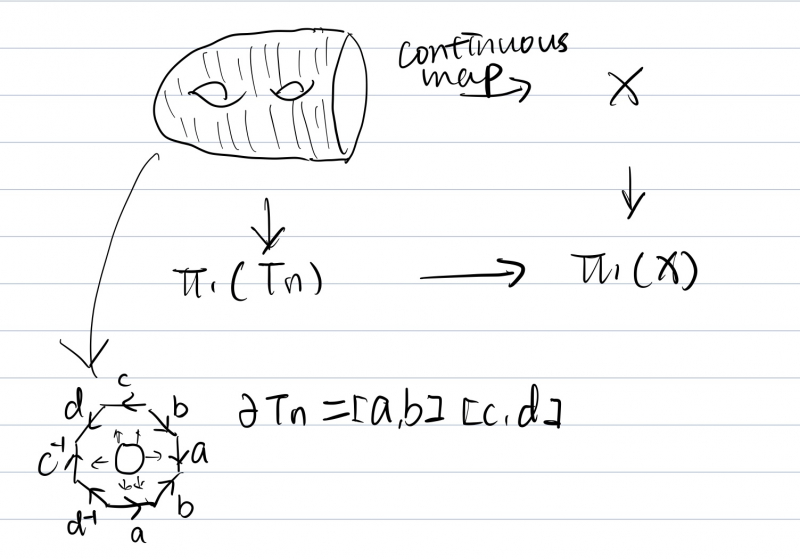
Here, π1(S)π1(S) is a free group of rank 2k2k and the boundary loop is a product of kk commutators, which under the map represents the word.
This relation between surface maps and cl can be translated and improved to the following topological definition of scl.
Definition:
sclG(g)=inf−χ(S)2n(S)sclG(g)=inf−χ(S)2n(S)
where the infimum is taken over compact oriented surfaces SS without sphere or disk components, mapped in to XX so that each boundary represents a power of gg. Here χ(S)χ(S) is the Euler characteristic, which for instance can be computed based on a triangulation of SS with VV vertices, EE edges and FF faces:
χ(S)=V−E+Fχ(S)=V−E+F
Here, n(S)n(S) denotes the degree of the surface, which is the total (algebraic) number of times the boundary “wraps around” gg.
Based on this topological definition, a remarkable theorem of Danny Calegari gives a way to compute the complicated invariant scl in free groups.
Theorem(Calegari): There is a polynomial time algorithm that computes sclG(g)sclG(g) for any gg in a free group GG.
Moreover, the nature of the algorithm shows that there is always a (connected) surface SS achieving the infimum in the topological definition. In particular, sclG(g)sclG(g) is always rational.
The idea of the proof uses a way to decompose surfaces into small pieces and turn the topological optimization problem into a linear programming problem (by finding the best combination of these small pieces).