Our algorithm should take in a list of generators for a matrix group and output valid ping pong intervals if they exist, or run forever otherwise. There are a few main things this will involve: finding initial intervals to start our search with, expanding the initial intervals, and checking whether there is valid containment among the intervals for ping pong.
How do we initialize intervals?
We want to consider generators who have attracting and repelling eigenvalues. This will make the intervals easier to find since we can predict what their actions will look like on RP1RP1. The eigenvector corresponding to the attracting eigenvalue will remain as a fixed point and pull the rest of RP1RP1 closer to it. This means the eigenvector corresponding to the repelling eigenvalue will be a fixed point for the inverse of the generator. So we can choose our intervals to be some epsilon neighborhood of these eigenvectors in RP1RP1.
Given two generators that lie in the SL(2,R)SL(2,R) (the group of 2×22×2 matrices with real entries that have determinant 1), we found 2 eigenvectors for each generators. Let v0v0 and v1v1 be the components of each eigenvector. These eigenvectors were mapped from the real projective line (RP1RP1) onto the unit circle (S1S1) via the homeomorphism

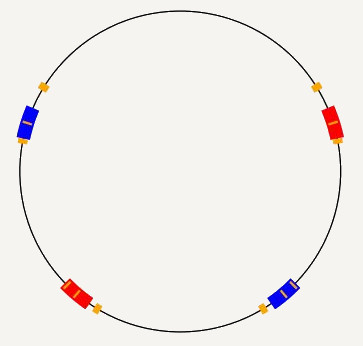
Figure 1: Here is an example of what the initial intervals might look like along with the images of these
intervals under the other generators. (Each color corresponds to a generator and its inverse)

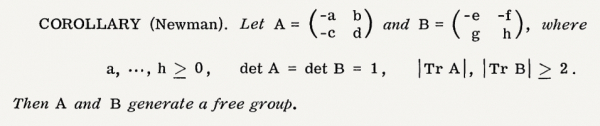
To create nn generators which generate a free group, we use the fact that all free groups of n≥3n≥3 generators are subgroups of a free group on 2 generators. In fact, if AA and BB generate a free group, then AkBk,k≤nAkBk,k≤n generate a free group. So we can reuse this corollary to get AA and BB and then use these to find the nn generators we want.
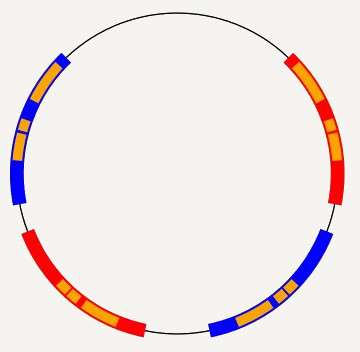
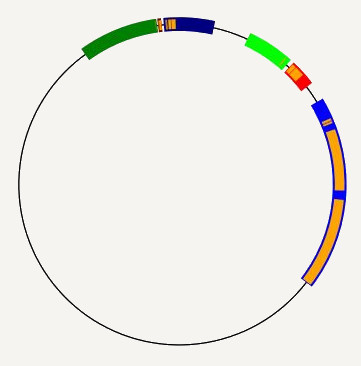
Figure 2: Examples of valid ping pong intervals. (1): Linear expansion for 2 generators, (2): Geometric expansion for 3 generators.
See the code on GitHub here: https://github.com/CapSnCrunch/TXGL
