SL(2,R) Action Viewer
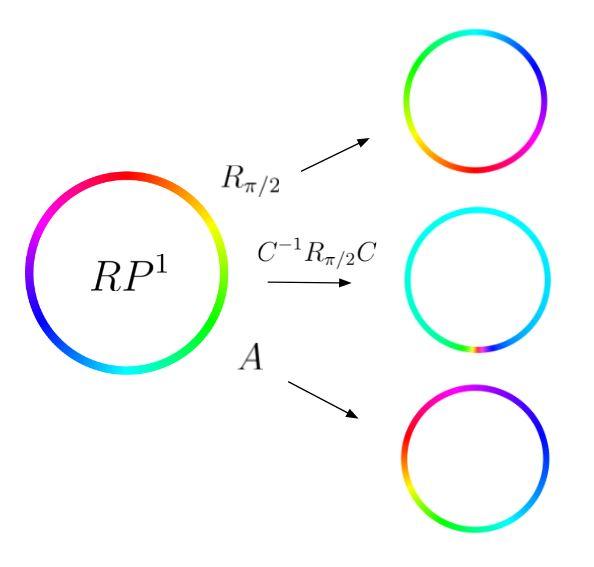
Tool designed to help visualize the action of matrices on RP1. A is a matrix in the representation of a Triangle Group.
Searching for Intervals (Linear Expansion)
Intervals for the (3,3,4)-Triangle Group
Searching for Intervals (Image Patching)
At this point, we’ve successfully created an algorithm that can find valid generalized ping-pong intervals in RP1RP1 for a representation of certain strongly geodesically automatic into SL(2,R)SL(2,R), and have the foundations of a method for computing an upper bound on the size of the kernel of this representation. However, there are still a few unfinished pieces to this project.
Exploring Image Patching
Because containment rules for generalized ping-pong don’t require that intervals are disjoint or connected, we implemented “image patching” as a search algorithm to find valid intervals. While image patching is much faster than linear expansion and seems generally promising, it still doesn’t fully work for the triangle group. Moreover, as we test more complex groups, the intervals become difficult to visualize with our current program’s output. In order to resolve the current issues with image patching, we’ll need to first rework our visualizations to investigate what the specific problems are, and then we can work on finding a resolution to ensure that image patching functions correctly.
Explicit Upper Bound for Size of the Kernel
Once the program has found valid intervals, it guarantees that there is some finite upper bound on the size of the kernel. As previously discussed, finding this upper requires calculating two values: λλ and CC. We’ve mostly developed a method to find λλ, but there are still a few steps of calculus that we haven’t yet implemented into the program. As for CC, while it should be theoretically easier to calculate, we haven’t done much work on explicitly finding this value. Once λλ and CC are found, the upper bound can be calculated, which will determine the faithfulness of the representation.
Extending the Algorithm to SL(n,R)SL(n,R) and RPn−1RPn−1
Currently, the algorithm supposes that the representation is into SL(2,R)SL(2,R), and acts on RP1RP1. However, we should be able to extend it to generalized nn. This would mean adjusting the algorithm so it searches for intervals in RPn−1RPn−1, which would verify the faithfulness of a representation into SL(n,R)SL(n,R). For example, in the case n=3n=3, we’d work with a representation into SL(3,R)SL(3,R) and search for valid regions in RP2RP2. Perhaps this will be “better” in some sense for finding intervals for certain groups.
Unlike the ping pong lemma, finding valid intervals for generalized ping pong leaves us with a bit more work to do. As covered in the Generalized Ping Pong section, we are left with a bound on the size of the kernel instead of knowledge that that kernel is just 0. After finding valid intervals, we can theoretically compute what this upper bound is and then simply check all words of length up to a number related to that bound in order to officially verify the faithfulness of the representation.
The paper ‘Uniform Hyperbolic Finite-Valued SL(2,R)-Cocycles‘ outlines this bound in Chapter 2 but does not give a means of explictly computing it. In order to get a numerical bound as a function of our valid intervals, we need to solve for two separate values: λλ and CC. We’ve found this to be quite a lot of work to do, so we’ve finished some of the calculation for λλ and left finding CC for future work.
The algorithm takes as input a list of generators in SL(2,R)SL(2,R) along with a directed graph representing the automatic structure of the group the generators represent. As output, we want a set of intervals in RP1RP1 which satisfy the containment dictated by the automatic structure or for the program to run forever in attempt to find them. As with the last project, this involves a few primary steps: initializing intervals, expanding the intervals, and checking for valid containments.
Initializing Intervals
In the previous project, since an image of an interval under some generators needed to be contained back in the interval itself, we knew that the eigenvector of the generator in RP1RP1 would need to be contained in that interval (since it wouldn’t move under the action of that generator). In this case however, not all of the matrices we are using have real eigenvalues (for example, a representation of a cyclic free product uses rotation matrices which have complex eigenvalues).
Instead, we generalize to the singular directions of these matrices. The valid intervals should contain the limits of singular directions of words of infinite length in our group. We approximate this by taking words of some set length (usually length 5 or 6 does the trick).
Each vertex of the automatic structure requires its own interval, so we find all words of length 5 which can be generated by starting at a particular vertex and then find the larger singular direction of the matrix representing each of those words. A disconnected interval is initialized as the union of epsilon balls around each of these singular directions.
Figure 1: A set of intervals initialized around singular directions of words from the automatic structure.
Interval Expansion
There are a few approaches to expanding these initialized intervals in search of valid ones: linear expansion, geometric expansion, and image patching. We created the geometric expansion approach in the last project because of the constraint that intervals must be disjoint. By expanding some percentage of the distance between an intervals nearest neighbor, it was never able to intersect with others. In our generalized version of ping pong however, there is no such requirment, so geometric expansion isn’t necessarily required.
Method 1: Linear Expansion
Linear expansion works by checking which intervals fail containments (an image they need to contain is poking out somewhere) and expanding each endpoint of the interval by some set amount ϵϵ. This works fairly well and is able to find valid intervals for many of the simpler groups we tried (free products of cyclic groups of order <= 10). However, when the groups are more complex and have large automatic structures that apply many constraints, it’s easy to accidentally jump past a set of valid intervals by expanding too much in a particular direction. For example, the (3,3,4)-Triangle group has a structure with around 15 vertices and 40 edges. We are currently attempting to find a search method that works for these more complex groups, starting with the rather promising image patching method.
Method 2: Image Patching
We eliminated the need for geometric expansion because of the removal of the requirement for disjointness between intervals. In generalizing ping pong, we also eliminate another constraint; the intervals themselves don’t need to be connected. Linear expansion doesn’t take advantage of this as well because although an interval may start disconnected after initialization, it can never create new components that it may need. Image patching solves this issue by extending each interval to include exactly the amount of space it needs to in order to satisfy containment constraints at each step. For example, if image AIaAIa needs to be contained in IbIb, we redefine IbIb as the union Ib∪AIaIb∪AIa. This way, we are making the minimum necessary expansion to satisfy containment at each step.
Expanding in this way can still cause issues that we are trying to deal with though. The method works even faster than Linear Expansion for cyclic free products (only ~4 expansion steps as opposed to a couple hundred) but still does not work for the triangle group. We believe it may have to do with the order in which we expand the intervals by patching.
Checking Containment
Checking containment is not hard. To see if a particular image is contained in another interval, we simply need to loop through all components of the image and check if each one is contained in at least one component of the desired interval. It is important to note though that issues may arise if we expand previously disconnected components to intersect with one another. In order to check containment from here, we need to first combine these into a single component, but this check is another simple loop across the components of the interval.
Testing the Algorithm
In order to see if the algorithm works, we need a set of test inputs. We made a generator for cyclic free products of any pair of orders where the matrices are conjugated rotations and the automatic structure is created by iteratively adding vertices and edges to an easier to construct graph for the cyclic free product of orders 2 and 3.
Figure 2: Some valid intervals for a cyclic free product of orders 2 and 3.
The intervals on the left are found with Linear Expansion and the right is found with Image Patching.
Note that there are multiple sets of intervals which satisfy all the required containment constraints.
See the code on GitHub here: https://github.com/CapSnCrunch/TXGL
