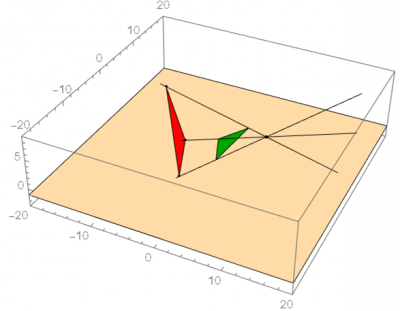
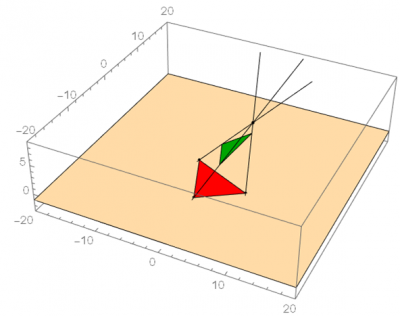
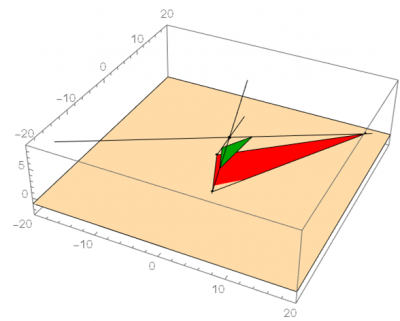
This project began with an observational experiment which expanded into projective space as we learned more about projective linear transformations. We first set out to determine the types of triangles which could be projected by a flat, equilateral triangle given a movable point source. As seen below, we could orient the point source in any relation to the triangle, and we observed the resulting projections on some arbitrary plane (in this example, the z = 0 plane). Depending on how we rotated the triangle and positioned the point source, the size and shape of the shadow changed. We repeated this experiment with various kinds of triangles, and found that any type of triangle could be projected regardless of the characteristics of the original triangle. In other words, nothing about the size or side lengths of a triangle could be determined by simply observing its shadow.
We calculated the orientation of the triangle based on nine parameters: three parameters corresponding to the position of the point source, and two parameters for each of the vertices of the triangle. We described the vertices of the projection using lines extending from the point source through the vertices of the triangle and intersecting with the observation plane.
Below: various triangles could be projected (in red) with a constant original triangle (in green).