
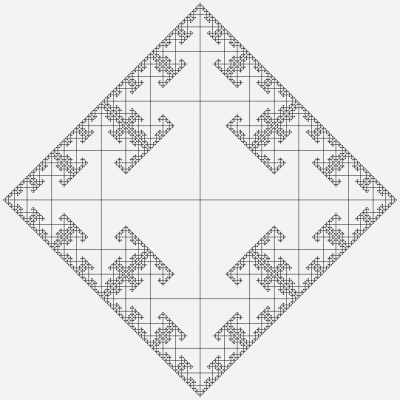
Figure 1: Cayley graph for a free group on 2 generators.
By recursively cheking through all of the points of the Cayley graph, we can try to find if any word in GG is equivalent to the identity, ie. if there are any relations. If a relationship is found, we will know that GG is not a free group; however, searching the Cayley graph will run forever if GG is a free group, since the algorithm has an infinite amount of words in the group to check. In other words (no pun intended), the program will continue to search for relations that do not exist. Then, we need to find another algorithm which will instead terminate in finite time when GG is free. This requires the use of the Ping-Pong lemma, and a consequence of using this method is that the program will run indefinetely if the group is not free.





