This test is used to determine if the observed frequencies of a single categorical variable with two or more levels matches some expected distribution. The test statistic for this method measures the differences in the observed frequencies of each level of the variable compared to the expected frequencies under the claimed distribution.
Assumptions:
- Random samples
- Independent observations
- The sample size is large enough such that all expected frequencies are greater than 1 and at least 80% are greater than 5.
If your data violates the sample size assumption, try combining some of your groups together to increase the expected frequencies.
Hypotheses:
Ho: The observed distribution of the variable matches the expected distribution.
HA: The observed distribution of the variable differs from the expected distribution.
Relevant Equations:
Degrees of freedom: number of categories – 1
Example 1: Hand calculation
This video analyzes if the observed distribution of pea plants matched the expected distribution from Mendel’s pea plant experiment.


Sample conclusion: After checking the assumptions of random sampling and noting that none of the expected counts for our data were less than 5, we completed a chi-square test of goodness of fit to determine if the distribution of pea plants matched what we expected, which was that 3/4 of the pea plants were yellow and 1/4 were green. We failed to reject the null hypothesis and found evidence that the distributions did not differ (X2 (df=1)=1.31, p>.05).
Example 2: Performing analysis in Excel 2016 on
These videos analyze if the distribution of participants’ favorite superhero matches the expected distribution.
To calculate a chi-square test in Excel, you must first create a frequency table of the data. The first video below describes this process. The second video runs the chi-square test.
Frequency table:
PDF directions corresponding to video
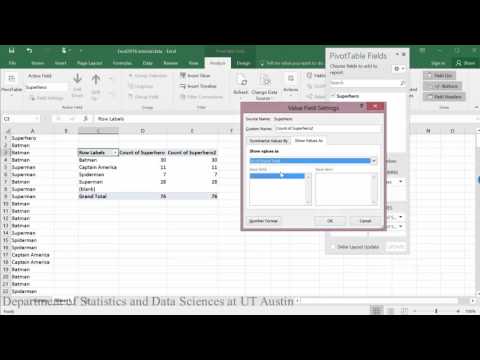

Goodness of fit test:
PDF directions corresponding to video


Sample conclusion: After checking the assumptions of random sampling and noting that none of the expected counts for our data were less than 5, we completed a chi-square test of goodness of fit to determine if the distribution of superheros matched what we expected, which was that all superheros would be equally selected. We rejected the null hypothesis and found evidence that the distribution we achieved did differ from that which was expected (X2 (df=3)=21.58, p<.001).
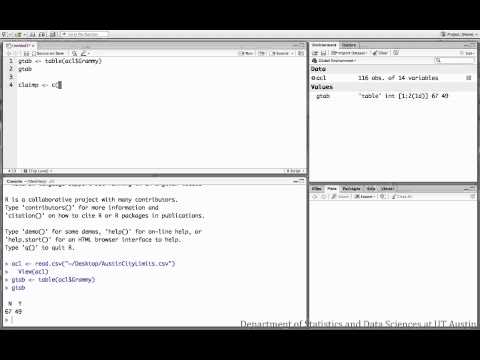
Example 3: Performing analysis in R
This dataset is about musicians who participated in the Austin City Limits music festival. This video investigates the claim that 1/3 of all ACL participants have won a Grammy.
Dataset used in video
R script file used in video