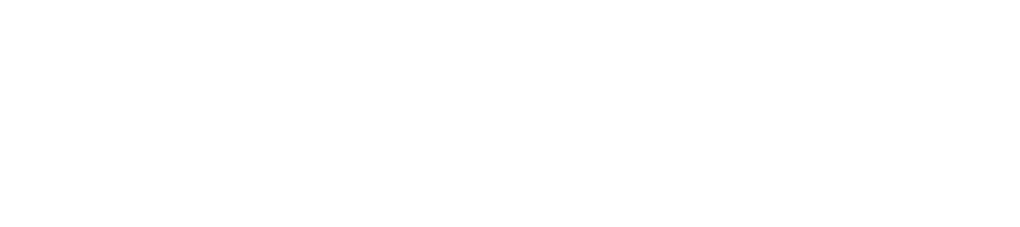A paired t-test can be run on a variable that was measured twice for each sample subject to test if the mean difference in measurements is significantly different from zero. For example, consider a sample of people who were given a pre-test measuring their knowledge of a topic. Then, they were given a video presentation about the topic, and were tested again afterwards with a post-test:
| Sample Subject | Pre-Test Score | Post-Test Score | Difference |
| 1 | 10 | 18 | 8 |
| 2 | 14 | 12 | -2 |
| 3 | 15 | 15 | 0 |
| … |
A paired t-test can determine if the mean of the pre-test scores is significantly different than the mean of their post-test scores by testing if the mean difference in scores for these subjects was different from zero. Although the paired t-test is considered a “two-sample” t-test, it is actually the same as running a one-sample t-test on the differences.
Hypotheses:
Ho: The difference in population means equals zero, or μd = 0
HA: The difference in population means does not equal zero, or μd ≠ 0
This test can also be conducted with a directional alternate hypothesis such as:
Ho: The difference in population means equals zero, or μd = 0
Ha: The difference in population means is greater than zero, or μd > 0
Relevant equations:
Degrees of freedom: number of pairs – 1
The test statistic (where dbar is the sample mean difference and SE is the estimated standard error of the differences):
For more information on how to calculate the sample mean and standard deviation, see this page.
Assumptions:
- Random samples
- Independent observations
- The differences are normally distributed.
If the third assumption is violated, an alternative test is the Sign Test, which tests if the median difference significantly differs from zero.
Example 1: Hand calculation video
This example uses a paired t-test to determine if drinking coffee significantly increases blood pressure.


Example 2: How to run in Excel 2016 on
Some of this analysis requires you to have the add-in Data Analysis ToolPak in Excel enabled.
In this tutorial you will determine if students performed differently on the pre- versus post-stats test.
Dataset used in video
PDF directions corresponding to video


Example 3: How to run in RStudio
This example tests if there was change in how likely (on a scale of 1-10) students felt they would be in an exclusive relationship at the end of the year from the beginning of the semester compared to at the end.
Dataset used in video
R script file used in video