In order to give a proper introduction to Gaussian kernels, this week’s post is going to start out a little bit more abstract than usual. This level of abstraction isn’t strictly necessary to understand how Gaussian kernels work, but the abstract perspective can be extremely useful as a source of intuition when trying to understand probability distributions in general. So here’s the deal: I’ll try to build up the abstraction slowly, but if you ever get hopelessly lost, or just can’t take it any more, you can skip down to the heading that says “The practical part” in bold – That’s where I’ll switch to a more concrete description of the Gaussian kernel algorithm. Also, if you’re still having trouble, don’t worry too much – Most of the later posts on this blog won’t require that you understand Gaussian kernels, so you can just wait for next week’s post (or skip to it if you’re reading this later on).
Recall that a kernel is a way of placing a data space into a higher dimensional vector space so that the intersections of the data space with hyperplanes in the higher dimensional space determine more complicated, curved decision boundaries in the data space. The main example that we looked at was the kernel that sends a two-dimensional data space to a five-dimensional space by sending each point with coordinates  to the five-dimensional point with coordinates
to the five-dimensional point with coordinates  . If we wanted to give ourselves even more flexibility, we could pick an even higher dimensional kernel, for example by sending the point
. If we wanted to give ourselves even more flexibility, we could pick an even higher dimensional kernel, for example by sending the point  to the point
to the point  in a nine-dimensional space.
in a nine-dimensional space.
This week, we’re going to go beyond higher dimensional vector spaces to infinite-dimensional vector spaces. You can see how the nine-dimensional kernel above is an extension of the five-dimensional kernel – we’ve essentially just tacked on four more dimensions at the end. If we keep tacking on more dimensions in this way, we’ll get higher and higher dimensional kernels. If we were to keep doing this “forever”, we would end up with infinitely many dimensions. Note that we can only do this in the abstract. Computers can only deal with finite things, so they can’t store and process computations in infinite dimensional vector spaces. But we’ll pretend for a minute that we can, just to see what happens. Then we’ll translate things back into the finite world.
In this hypothetical infinite-dimensional vector space, we can add vectors the same way that we do with regular vectors, by just adding corresponding coordinates. However, in this case, we have to add infinitely coordinates. Similarly, we can multiply by scalars, by multiplying each of the (infinitely many) coordinates by a given number. We’ll define the infinite polynomial kernel by sending each point  to the infinite vector
to the infinite vector  . In particular, every monomial in the variables
. In particular, every monomial in the variables  and
and 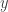 , such as
, such as  or
or  will appear in one of the entries of this kernel, possibly very far down the sequence.
will appear in one of the entries of this kernel, possibly very far down the sequence.
In order to get back to the computational world, we can recover our original five-dimensional kernel by just forgetting all but the first five of the entries. In fact, the original five-dimensional space is contained in this infinite dimensional space. (The original five-dimensional kernel is what we get by projecting the infinite polynomial kernel into this five-dimensional space.)
Now take a deep breath, because we’re going to take this one step further. Consider, for a moment, what a vector is. If you ever took a mathematical linear algebra class, you may remember that vectors are officially defined in terms of their addition and multiplication properties. But I’m going to temporarily ignore that (with apologies to any mathematicians who are reading this.) In the computing world, we usually think of a vector as being a list of numbers. If you’ve read this far, you may be willing to let that list be infinite. But I want you to think of a vector as being a collection of numbers in which each number is assigned to a particular thing. For example, each number in our usual type of vector is assigned to one of the coordinates/features. In one of our infinite vectors, each number is assigned to a spot in our infinitely long list.
But how about this: What would happen if we defined a vector by assigning a number to each point in our (finite dimensional) data space? Such a vector doesn’t pick out a single point in the data space; rather, once you pick this vector, if you point to any point in the data space, the vector tells you a number. Well, actually, we already have a name for that: Something that assigns a number to each point in the data space is a function. In fact, we’ve been looking at functions a lot on this blog, in the form of density functions that define probability distributions. But the point is, we can think of these density functions as vectors in an infinite-dimensional vector space.
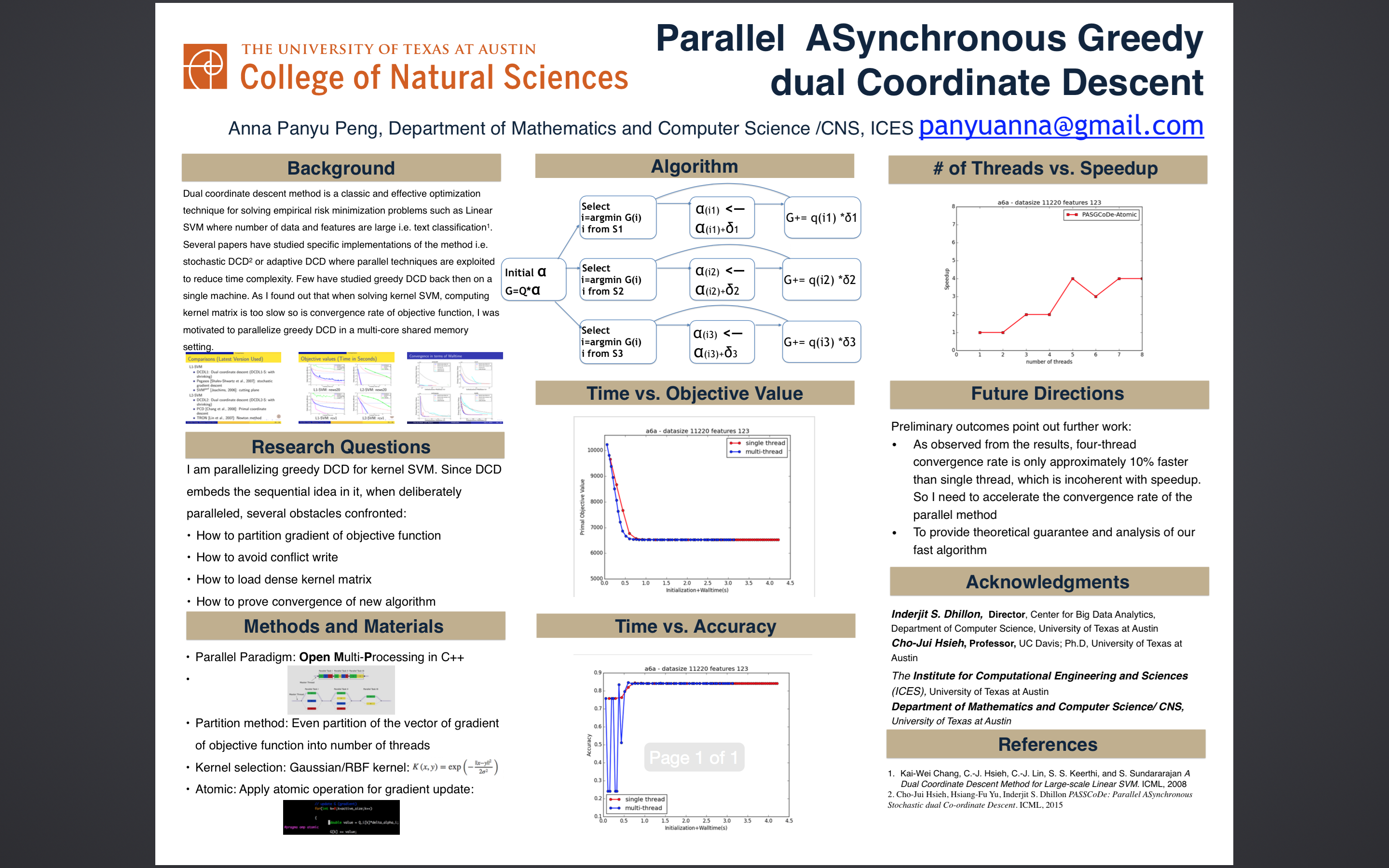
How can a function be a vector? Well, we can add two functions by just adding their values at each point. This was the first scheme we discussed for combining distributions in last week’s post on mixture models. The density functions for two vectors (Gaussian blobs) and the result of adding them are shown in the Figure below. We can multiply a function by a number in a similar way, which would result in making the overall density lighter or darker. In fact, these are both operations that you’ve probably had lots of practice with in algebra class and calculus. So we’re not doing anything new yet, we’re just thinking about things in a different way.

The next step is to define a kernel from our original data space into this infintie dimensional space, and here we have a lot of choices. One of the most common choices is the Gaussian blob function which we’ve seen a few times in past posts. For this kernel, we’ll choose a standard size for the Gaussian blobs, i.e. a fixed value for the deviation 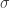 . Then we’ll send each data point to the Gaussian function centered at that point. Remember we’re thinking of each of these functions as a vector, so this kernel does what all kernels do: It places each point in our original data space into a higher (in fact, infinite) dimensional vector space.
. Then we’ll send each data point to the Gaussian function centered at that point. Remember we’re thinking of each of these functions as a vector, so this kernel does what all kernels do: It places each point in our original data space into a higher (in fact, infinite) dimensional vector space.
Now, here’s the problem: In order to bring things back to the computational world, we need to pick out a finite dimensional vector space sitting in this infinite dimensional vector space and “project” the infinite dimensional space into the finite dimensional subspace. We’ll choose a finite-dimensional space by choosing a (finite) number of points in the data space, then taking the vector space spanned by the Gaussian blobs centered at those point. This is the equivalent of the vectors pace defined by the first five coordinates of the infinite polynomial kernel, as above. The choice of these points is important, but we’ll return to that later. For now, the question is how do we project?
For finite dimensional vectors, the most common way to define a projection is by using the dot product: This is the number that we get by multiplying corresponding coordinates of two vectors, then adding them all together. So, for example the dot product of the three-dimensional vectors  and
and  is
is  .
.
We could do something similar with functions, by multiplying the values that they take on corresponding points in the data set. (In other words, we multiply the two functions together.) But we can’t then add all these numbers together because there are infinitely many of them. Instead, we will take an integral! (Note that I’m glossing over a ton of details here, and I again apologize to any mathematicians who are reading this.) The nice thing here is that if we multiply two Gaussian functions and integrate, the number is equal to a Gaussian function of the distance between the center points. (Though the new Gaussian function will have a different deviation value.)
In other words, the Gaussian kernel transforms the dot product in the infinite dimensional space into the Gaussian function of the distance between points in the data space: If two points in the data space are nearby then the angle between the vectors that represent them in the kernel space will be small. If the points are far apart then the corresponding vectors will be close to “perpendicular”.
The practical part
So, lets review what we have so far: To define an 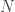 -dimensional Gaussian kernel, we first choose
-dimensional Gaussian kernel, we first choose 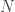 points in the data space. We can then calculate the kernel coordinates of any point in the data space by calculating its distance to each of these chosen data points and taking the Gaussian function of the distances.
points in the data space. We can then calculate the kernel coordinates of any point in the data space by calculating its distance to each of these chosen data points and taking the Gaussian function of the distances.
To better understand how this kernel works, lets figure out what the intersection of a hyperplane with the data space looks like. (This is what is done with kernels most of the time, anyway.) Recall that a plane is defined by an equation of the form  where
where  are the coordinates of the point (in the higher dimensional kernel space) and
are the coordinates of the point (in the higher dimensional kernel space) and  are parameters that define the hyperplane. If we’re using a Gaussian kernel then, thanks to our version of the dot product, the values
are parameters that define the hyperplane. If we’re using a Gaussian kernel then, thanks to our version of the dot product, the values  measure the distances to our
measure the distances to our 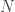 chosen points. The decision boundary is thus the set of points for which the Gaussian function of the distances to these
chosen points. The decision boundary is thus the set of points for which the Gaussian function of the distances to these 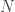 points satisfy this equation.
points satisfy this equation.
That’s still pretty hard to unpack, so lets look at an example where each of the values  is either 1 or -1. Then near each data point with label
is either 1 or -1. Then near each data point with label  , the value
, the value 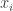 will be very close to 1, while the other values
will be very close to 1, while the other values  will be small, so the sum
will be small, so the sum  will be positive. Similarly, near a point with
will be positive. Similarly, near a point with  , the sum will be negative. Thus if
, the sum will be negative. Thus if  then the decision boundary will separate the positive points from the negative points. In fact, it will carve out a region reminiscent of the Gaussian balls that define the kernel. One example is indicated on the left in the Figure below, where the colors indicate whether the coefficients are positive or negative. As you can see, the result looks something like a smooth version of the nearest neighbors algorithm.
then the decision boundary will separate the positive points from the negative points. In fact, it will carve out a region reminiscent of the Gaussian balls that define the kernel. One example is indicated on the left in the Figure below, where the colors indicate whether the coefficients are positive or negative. As you can see, the result looks something like a smooth version of the nearest neighbors algorithm.

If we adjust the parameters  , this has the effect of changing the sizes of the Gaussian balls around the points, and thus moves the decision boundary towards or away from them, as on the right of the Figure. If a coefficient switches from positive to negative, the decision boundary will move from one side of a point to the other. If we have a labeled data set (which may or may not coincide with the
, this has the effect of changing the sizes of the Gaussian balls around the points, and thus moves the decision boundary towards or away from them, as on the right of the Figure. If a coefficient switches from positive to negative, the decision boundary will move from one side of a point to the other. If we have a labeled data set (which may or may not coincide with the 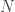 points that define the Gaussian kernel) then training a linear classification algorithm (such as SVM or logistic regression) in the kernel space corresponds to moving this decision boundary around, within the constraints defined above, to maximize how many of the data points are on the correct side.
points that define the Gaussian kernel) then training a linear classification algorithm (such as SVM or logistic regression) in the kernel space corresponds to moving this decision boundary around, within the constraints defined above, to maximize how many of the data points are on the correct side.
So, this gives us more flexibility for choosing the decision boundary (or, at least, a different kind of flexibility) but the final result will be very dependent on the 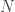 vectors that we choose. If we choose too many (such as if we let the
vectors that we choose. If we choose too many (such as if we let the 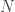 points that define the kernel be the same as the data points) then we will risk overfitting, similar to how the nearest neighbor algorithm tends to lead to overfitting. What we really want is a small number of points that are evenly distributed throughout the set, ideally such that each of the
points that define the kernel be the same as the data points) then we will risk overfitting, similar to how the nearest neighbor algorithm tends to lead to overfitting. What we really want is a small number of points that are evenly distributed throughout the set, ideally such that each of the 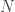 points is close to mostly points in the same class.
points is close to mostly points in the same class.
Finding such a collection of points is a very different problem from what we’ve been focusing on in the posts so far on this blog, and falls under the category of unsupervised learning/descriptive analytics. (In the context of kernels, it can also be thought of as feature selection/engineering.) In the next few posts, we’ll switch gears and start to explore ideas along these lines.