Following up on Part 1 and Part 2, and Part 3, it is time to into the ugly stuff — trying to control DRAM bank and rank access patterns and working to improve the effectiveness of the memory controller prefetcher.
Background: Banks and Ranks
The DRAM installed in the system under test consists of 2 dual-rank 2GiB DIMMs in each channel of each chip. Each “rank” is composed of 9 DRAM chips, each with 1 Gbit capacity and each driving 8 bits of the 72-bit output of the DIMM (64 bits data + 8 bits ECC). Each of these 1 Gbit DRAM chips is divided into 8 “banks” of 128 Mbits each, and each of these banks has a 1 KiB “page size”. This “DRAM page size” is unrelated to the “virtual memory page size” discussed above, but it is easy to get confused! The DRAM page size defines the amount of information transferred from the DRAM array into the “open page” buffer amps in each DRAM bank as part of the two-step (row/column) addressing used to access the DRAM memory. In the system under test, the DRAM page size is thus 8 KiB– 8 DRAM chips * 1 KiB/DRAM chip — with contiguous cache lines distributed between the two DRAM channels (using a 6-bit hash function that I won’t go into here). Each DRAM chip has 8 banks, so each rank maps 128 KiB of contiguous addresses (2 channels * 8 banks * 8 KiB/bank).
Why does this matter?
- Every time a reference is made to a new DRAM page, the full 8 KiB is transferred from the DRAM array to the DRAM sense amps. This uses a fair amount of power, and it makes sense to try to read the entire 8 KiB while it is in the sense amps. Although it is beyond the scope of today’s discussion, reading data from “open pages” uses only about 1/4 to 1/5 of the power required to read the same amount of data in “closed page” mode, where only one cache line is retrieved from each DRAM page.
- Data in the sense amps can be accessed at significantly lower latency — this is called “open page” access (or a “page hit”), and the latency is referred to as the “CAS latency”. On most systems the CAS latency is between 12.5 ns and 15 ns, independent of the frequency of the DRAM bus. If the data is not in the sense amps (a “page miss”), loading data from the array to the sense amps takes an additional latency of 12.5 to 15 ns. If the sense amps were holding other valid data, it would be necessary to write that data back to the array, taking an additional 12.5 to 15 ns. If the DRAM latency is not completely overlapped with the cache coherence latency, these increases will reduce the sustainable bandwidth according to Little’s Law: Bandwidth = Concurrency / Latency
- The DRAM bus is a shared bus with multiple transmitters and multiple receivers — five of each in the system under test: the memory controller and four DRAM ranks. Every time the device driving the bus needs to be switched, the bus must be left idle for a short period of time to ensure that the receivers can synchronize with the next driver. When the memory controller switches from reading to writing this is called a “read/write turnaround”. When the memory controller switches from writing to reading this is called a “write/read turnaround”. When the memory controller switches from reading from one rank to reading from a different rank this is called a “chip select turnaround” or a “chip select stall”, or sometimes a “read-to-read” stall or delay or turnaround. These idle periods depend on the electrical properties of the bus, including the length of the traces on the motherboard, the number of DIMM sockets, and the number and type of DIMMs installed. The idle periods are only very weakly dependent on the bus frequency, so as the bus gets faster and the transfer time of a cache line gets faster, these delays become proportionately more expensive. It is common for the “chip select stall” period to be as large as the cache line transfer time, meaning that a code that performs consecutive reads from different banks will only be able to use about 50% of the DRAM bandwidth.
- Although it could have been covered in the previous post on prefetching, the memory controller prefetcher on AMD Family10h Opteron systems appears to only look for one address stream in each 4 KiB region. This suggests that interleaving fetches from different 4 KiB pages might allow the memory controller prefetcher to produce more outstanding prefetches. The extra loops that I introduce to allow control of DRAM rank access are also convenient for allowing interleaving of fetches from different 4 KiB pages.
Experiments
Starting with Version 007 (packed SSE arithmetic, large pages, no software prefetching) at 5.392 GB/s, I split the single loop over the array into a set of three loops — the innermost loop over the 64 cache lines in a 4 KiB page, a middle loop for the 32 4 KiB pages in a 128 KiB DRAM rank, and an outer loop for the (many) 128 KiB DRAM rank ranges in the full array. The resulting Version 008 loop structure looks like:
for (k=0; k<N; k+=RANKSIZE) {
for (j=k; j<k+RANKSIZE; j+=PAGESIZE) {
for (i=j; i<j+PAGESIZE; i+=8) {
x0 = _mm_load_pd(&a[i+0]);
sum0 = _mm_add_pd(sum0,x0);
x1 = _mm_load_pd(&a[i+2]);
sum1 = _mm_add_pd(sum1,x1);
x2 = _mm_load_pd(&a[i+4]);
sum2 = _mm_add_pd(sum2,x2);
x3 = _mm_load_pd(&a[i+6]);
sum3 = _mm_add_pd(sum3,x3);
}
}
}
The resulting inner loop looks the same as before — but with the much shorter iteration count of 64 instead of 512,000:
..B1.30:
addpd (%r14,%rsi,8), %xmm3
addpd 16(%r14,%rsi,8), %xmm2
addpd 32(%r14,%rsi,8), %xmm1
addpd 48(%r14,%rsi,8), %xmm0
addq $8, %rsi
cmpq %rcx, %rsi
jl ..B1.30
The overall performance of Version 008 drops almost 9% compared to Version 007 — 4.918 GB/s vs 5.392 GB/s — for reasons that are unclear to me.
Interleaving Fetches Across Multiple 4 KiB Pages
The first set of optimizations based on Version 008 will be to interleave the accesses so that multiple 4 KiB pages are accessed concurrently. This is implemented by a technique that compiler writers call “unroll and jam”. I unroll the middle loop (the one that covers the 32 4 KiB pages in a rank) and interleave (“jam”) the iterations. This is done once for Version 013 (i.e., concurrently accessing 2 4 KiB pages), three times for Version 014 (i.e., concurrently accessing 4 4 KiB pages), and seven times for Version 015 (i.e., concurrently accessing 8 4 KiB pages).
To keep the listing short, I will just show the inner loop structure of the first of these — Version 013:
for (k=0; k<N; k+=RANKSIZE) {
for (j=k; j<k+RANKSIZE; j+=2*PAGESIZE) {
for (i=j; i<j+PAGESIZE; i+=8) {
x0 = _mm_load_pd(&a[i+0]);
sum0 = _mm_add_pd(sum0,x0);
x1 = _mm_load_pd(&a[i+2]);
sum1 = _mm_add_pd(sum1,x1);
x2 = _mm_load_pd(&a[i+4]);
sum2 = _mm_add_pd(sum2,x2);
x3 = _mm_load_pd(&a[i+6]);
sum3 = _mm_add_pd(sum3,x3);
x0 = _mm_load_pd(&a[i+PAGESIZE+0]);
sum0 = _mm_add_pd(sum0,x0);
x1 = _mm_load_pd(&a[i+PAGESIZE+2]);
sum1 = _mm_add_pd(sum1,x1);
x2 = _mm_load_pd(&a[i+PAGESIZE+4]);
sum2 = _mm_add_pd(sum2,x2);
x3 = _mm_load_pd(&a[i+PAGESIZE+6]);
sum3 = _mm_add_pd(sum3,x3);
}
}
}
The assembly code for the inner loop looks like what one would expect:
..B1.30:
addpd (%r15,%r11,8), %xmm3
addpd 16(%r15,%r11,8), %xmm2
addpd 32(%r15,%r11,8), %xmm1
addpd 48(%r15,%r11,8), %xmm0
addpd 4096(%r15,%r11,8), %xmm3
addpd 4112(%r15,%r11,8), %xmm2
addpd 4128(%r15,%r11,8), %xmm1
addpd 4144(%r15,%r11,8), %xmm0
addq $8, %r11
cmpq %r10, %r11
jl ..B1.30
Performance for these three versions improves dramatically as the number of 4 KiB pages accessed increases:
- Version 008: one 4 KiB page accessed: 4.918 GB/s
- Version 013: two 4 KiB pages accessed: 5.864 GB/s
- Version 014: four 4 KiB pages accessed: 6.743 GB/s
- Version 015: eight 4 KiB pages accessed: 6.978 GB/s
Going one step further, to 16 pages accessed in the inner loop, causes a sharp drop in performance — down to 5.314 GB/s.
So this idea of accessing multiple 4 KiB pages seems to have significant merit for improving single-thread read bandwidth. Next we see if explicit prefetching can push performance even higher.
Multiple 4 KiB Pages Plus Explicit Software Prefetching
A number of new versions were produced
- Version 008 (single page accessed with triple loops) + SW prefetch yields Version 009
- Version 013 (two pages accessed) + SW prefetch –> Version 010
- Version 014 (four pages accessed) + SW prefetch –> Version 011
- Version 015 (eight pages accessed) + SW prefetch –> Version 012
In each case the prefetch was set AHEAD of the current pointer by a distance of 0 to 1024 8-Byte elements and all results were tabulated. Unlike the initial tests with SW prefetching, the results here are more variable and less easy to understand.
Starting with Version 009, the addition of SW prefetching restores the performance loss introduced by the triple-loop structure and provides a strong additional boost.
| loop structure | no SW prefetch | with SW prefetch |
| single loop | Version 007: 5.392 GB/s | Version 005: 6.091 GB/s |
| triple loop | Version 008: 4.917 GB/s | Version 009: 6.173 GB/s |
All of these are large page results except Version 005. The slight increase from Version 005 to Version 009 is consistent with the improvements seen in adding large pages from Version 006 to Version 007, so it looks like adding the SW prefetch negates the performance loss introduced by the triple-loop structure.
Combining SW prefetching with interleaved 4 KiB page access produces some intriguing patterns.
Version 010 — fetching 2 4KiB pages concurrently:
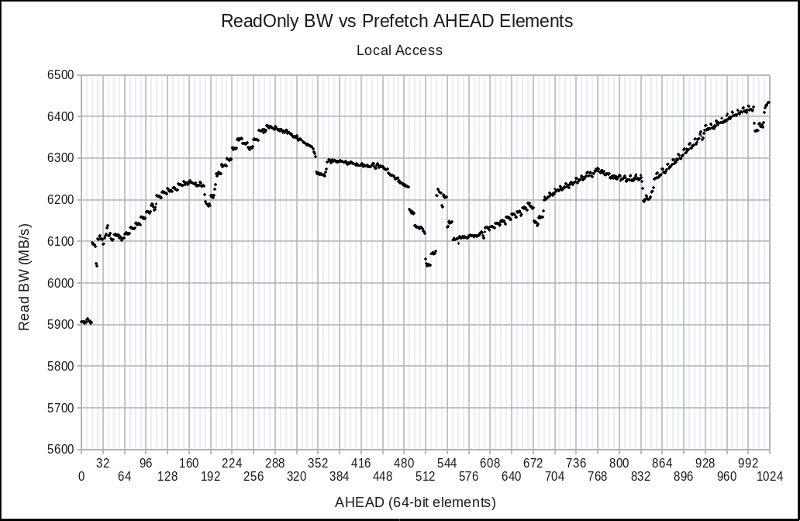
Version 011 — fetching 4 4KiB pages concurrently:

Version 012 — fetching 8 4KiB pages concurrently:
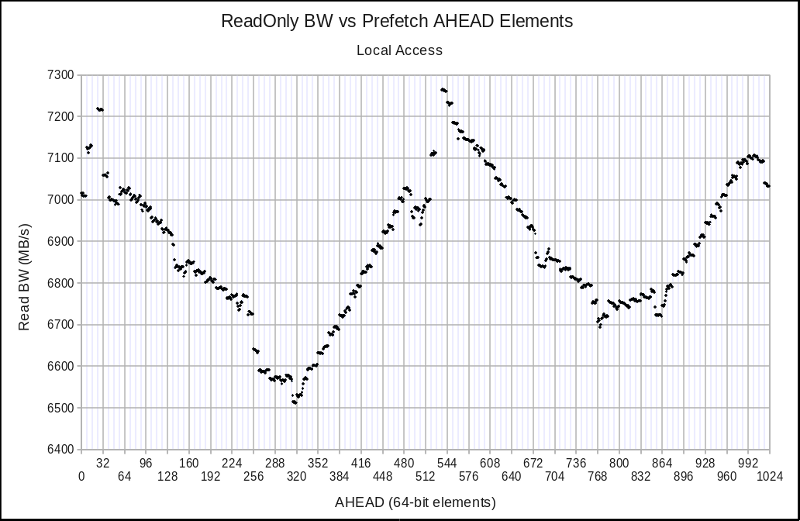
When reviewing these figures, keep in mind that the baseline performance number is the 6.173 GB/s from Version 009, so all of the results are good. What is most unusual about these results (speaking from ~25 years experience in performance analysis) is that the last two figures show some fairly strong upward spikes in performance. It is entirely commonplace to see decreases in performance due to alignment issues, but it is quite rare to see increases in performance that depend sensitively on alignment, but which remain repeatable and usable.
Choosing a range of optimum AHEAD distances for each case allows me to summarize:
| Pages Accessed in Inner Loop | no SW prefetch | with SW prefetch |
| 1 | Version 007: 5.392 GB/s | Version 009: 6.173 GB/s |
| 2 | Version 013: 5.864 GB/s | Version 010: 6.417 GB/s |
| 4 | Version 014: 6.743 GB/s | Version 011: 7.063 GB/s |
| 8 | Version 015: 6.978 GB/s | Version 012: 7.260 GB/s |
It looks like this is about as far as I can go with a single thread. Performance started at 3.401 GB/s and gradually increased to 7.260 GB/s — an increase of 113%. The resulting code is not terribly long, but it is important to remember that I only implemented the case that starts on a 128 KiB boundary (which is necessary to ensure that the accesses to multiple 4 KiB pages are all in the same rank). Extra prolog and epilog code will be required for a general-purpose sum reduction routine.
So why did I spend all of this time? Why not just start by running multiple threads to increase performance?
First, the original code was slow enough that even perfect scaling across four threads would barely provide enough concurrency to reach the 12.8 GB/s read bandwidth of the chip.
Second, the original code is not set up to allow control over which pages are being accessed. Using multiple threads that are accessing different ranks will significantly increase the number of chip-select stalls, and may not produce the desired level of performance. (More on this soon.)
Third, the system under test has only two DDR2/800 channels per chip — not exactly state of the art. Newer systems have two or four channels of DDR3 at 1333 or even 1600 MHz. Given similar memory latencies, Little’s Law tells us that these systems will only deliver more sustained bandwidth if they are able to maintain more outstanding cache misses. The experiments presented here should provide some insights into how to structure code to increase the memory concurrency.
But that does not mean that I won’t look at the performance of multi-threaded implementations — that is coming up anon…
