Earthquakes in subduction zones are controlled by a physical system that spans vast spatial and temporal scales, and the objectives of this project include figuring out on which scales processes are linked and what connections between the scales have to be considered in order to estimate likely rupture scenarios. However, our modeling efforts can be organized by several focus areas.
Watch Thorsten Becker’s talk Modeling Frameworks for Earthquake Deformation Problems – MTMOD from the 15th World Congress on Computational Mechanics & 8th Asian Pacific Congress on Computational Mechanics (WCCM-APCOM 2022). PDF of slides available here.
Short-term models
Such models capture the behavior of the megathrust interface over few seismic cycles and individual events, including the pre-, co- and post-seismic deformation on the surface as well as rupture propagation.
Working group leads: Gabriel and Johnson
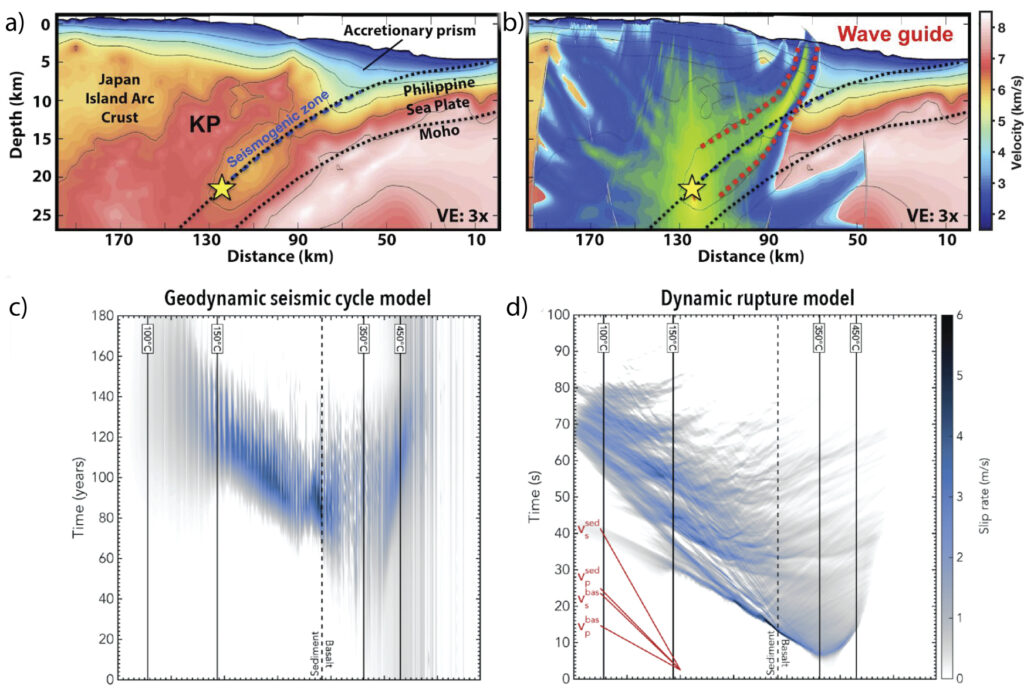
(a) P-wave tomography for the Kii Peninsula (Nankai); b) Radiation pattern (star: source, blue-green: seismic energy after 12 s). The low-velocity subduction channel acts as a wave-guide (A. Arnulf, pers. comm.). c) Slip rate evolution (colors) during a megathrust event in a 2-D geodynamic seismo-thermo-mechanical model and, d). for a coupled approach in which the fault conditions from c) are used in a fully dynamic rupture model. Note similarities in the rupture patterns, while time scales are very different. Rupture complexities result from lithological heterogeneity [van Zelst et al, 2019].
Long-term models
The plate boundary will evolve over time such that slab interface, topography, and the mantle wedge will evolve due to tectonic forcing and mantle convection. We seek to capture such processes from global to regional scales.
Working group leads: Becker and Lavier
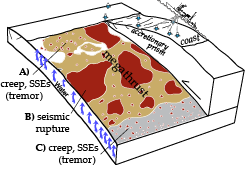
Megathrust cartoon with frictionally unstable (red) and (conditionally) stable regions (brown) [Lay et al., 2012; Burgmann, 2018]. Region A can display slow slip events (SSEs) and creep, but sometimes ruptures, as for the 2011 M9 Tohoku-Oki event. C is the site of SSEs, creep, and low frequency earthquakes in the transition from brittle to ductile behavior and likely facilitated by high (near hydrostatic) fluid pressure (blue arrows) [Behr and Burgmann, 2021].
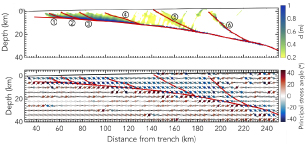
Accumulated slip, d, after modeled slip events in the sedimentary wedge with numbered splay faults (top) and principal compressive stress orientations [van Zelst et al., 2019].
Uncertainty quantification
One major challenge in terms of building physical models for megathrust hazard assessment is that there are major uncertainties as to material properties at depth as well as to the governing physical relationships. We therefore pursue a range of efforts to formally address uncertainties using parameter space exploration, reduced order modeling, and adjoint approaches.
Working group leads: Ghattas and May
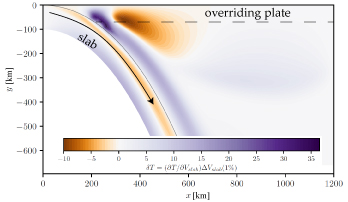
Example computation using Proper Orthogonal Decomposition to obtain non-intrusive derivatives using a reduced order model (ROM). Here, we show the sensitivity of slab, mantle, and plate inter-face temperature to subducting plate velocity for akinematic-dynamic upper mantle thermal computation [van Keken et al., 2008; England and Wilkins, 2004] (D. May, pers. comm.). The temperature field over the entire domain was used to define the ROM. However, one can, for example, now only evaluate the ROM along the plate interface for efficiency.
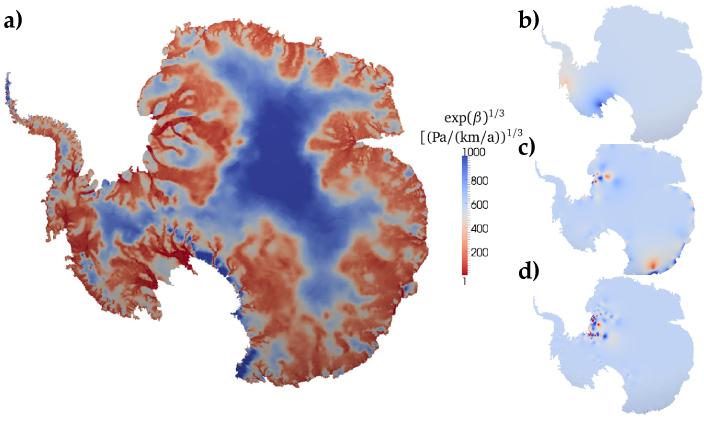
a) Uncertainty and data-relevance for the basal drag parameter for Antarctic ice sheet flow, achieved by solving the equations for a viscous fluid and using a low rank approximation of the parameter-to-observable map and adjoint-based actions of Hessians of the data misfit functional. This problem is closely related to the rupture prestress case. b-d) Eigenvectors of the data misfit Hessian corresponding to the 1st(b), 100th(c), and 500th(d) eigenvalues. Note that different eigenvectors localize in different regions and wavelengths. Modified from Isaac, et al., 2015.
Natural laboratories
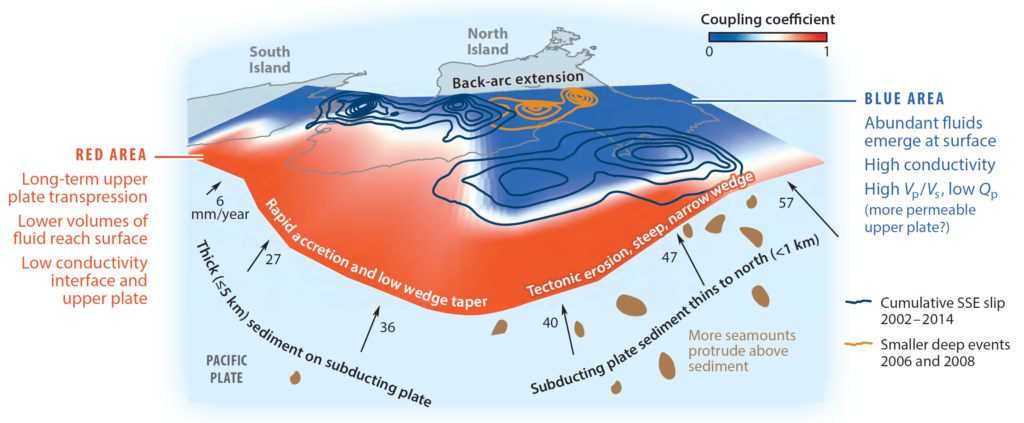
We will consider the natural laboratories of Japan (which hosts several trenches), New Zealand (Hikurangi margin), and the NW United States (Cascadia margin). These different regions show variable tectonic settings, including along strike, are in different stages of the seismic cycle, and are instrumented to variable degrees. By first verifying our models and then validating the general approach by cross-comparisons, we hope to arrive at a consistent description of megathrust systems.
Working group leads: Arnulf, Trugman, and Wallace